This won’t be a super-detailed post, but rather just a heads up that I stumbled across a new way to figure out the “threat” of meeting someone infected with COVID-19 while I’m out and about.
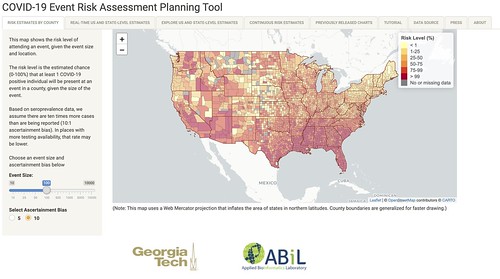
The smart folks over at Georgia Tech put together some research trying to unpack how likely it is that any one person meets another person infected with COVID-19. And they did this based on seroprevalence data. Researchers also assumed there are ten times more cases than are being reported (10:1 ascertainment bias). And while that may sound really overblown, keep in mind that many doctors have said that as many as 30- to 50-percent of cases may be asymptomatic. That is based on newer research than I’ve been using on this blog. On this blog, I have been more conservative, using the original research from cruise ships showing an asymptomatic rate around 33-percent. I do that for multiple reasons, but consistency being the main reason, since it is just an estimate.
But, I digress.
Georgia Tech estimates
Here is the percent-chance, according to the folks at Georgia Tech, that you run into someone that is infected with COVID-19 for a few cities (based on county-wide data) if you were to visit a grocery store with 50 people inside:
Mississippi
Gulfport: 79%
Hattiesburg: 93%
Laurel: 93%
Jackson: 97%
Meridian: 82%
Alabama
Birmingham: 93%
Huntsville: 92%
Montgomery: 93%
Mobile: 94%
Louisiana
Baton Rouge: 96%
New Orleans: 81%
Shreveport: 94%
That is pretty shocking. And at first, I was rather skeptical. But I did a little reading into the mathematics behind it, and it checks out.
From the researchers:
How we do our calculation:
What is the chance that one person at this event will already be infected with COVID-19? To answer this kind of question, we actually calculate the opposite. For example, if we were talking about a NFL game, we’d ask what is the chance that none of the 75,000 attendees is infected?
Let’s start by thinking about just one of them. If 20,000 of the 330 million people in the United States are sick, then each person has a 99.994% chance of being disease-free. In betting terms, the odds are 16,500:1 in our favor. While that sounds good from an individual perspective, the collective risk is very different.
In this scenario, the probability that all 75,000 attendees would have entered the stadium disease-free is like placing 75,000 bets each at nearly certain odds. Sure, you’ll win most of the bets. But the probability that you will win every single one of those bets is extremely low. To calculate it, we multiply the winning probability (1-1/16500) by itself 75,000 times and find that there is approximately a 1% chance that we win every time. In other words, the chances that one or more attendees would have arrived infected with SARS-CoV-2 is 99%.
This may be why the virus continues to spread so rapidly across the state of Mississippi. As people are slower to adopt wearing a mask while simultaneously attending large gatherings.

The above chart shows the percent-chance that someone – given the numbers from the entire state of Mississippi – at an event with 30 people is infected with the virus. This is made based on an estimate that there are roughly 16,000 currently-infected people in the state. It is a log scale, so it is tough to eyeball, but it is 15-percent.
Comparing that to my data
As many of you know, I’ve been trying to use estimates based on past research to keep a tally on how many people are currently sick, currently contagious. All of those estimates are based off of the numbers provided from the Mississippi Department of Health and research done previously regarding the number of asymptomatic cases given symptomatic cases on cruise ships (good petrie dishes), and the length of incubation period and illness from the CDC and other researchers.
Based on all of that data and research, there are an estimated 32,390 actively contagious people in the state of Mississippi. Contagious does not mean “sick” in this case as research has shown that people carry a viral load for up to two weeks after recovery, and are capable of infecting others still.
And again, that is an estimate.

If you take that into account, the per-cent chance that a person is carrying the virus increases to 28-percent in a group of 30 people. Better than a 1-in-4 shot.
Increase that to 100 people?

That bumps the chances up to more than 66-percent. About two-thirds.
What about on a football field, with 22 guys?

About a 21-percent chance. Roughly 1-in-5.
What does this mean?
It is important to note that this does not mean 1-in-4 people have the virus. I really want to drive this point home, too. Saying that on a football field that one out of every five players has the virus is wrong.
Rather, that one out of every five games played will feature at least one player who is capable of infecting others. Two out of every three grocery stores with 100 people will feature at least one person capable of infecting others. And one out of every four classrooms with 29 kids and one teacher will have at least one person capable of infecting others.
And again, these are just estimates. But these are estimates based on some reasonably basic math applied to research isn’t perfect, but has been reproduced multiple times.
Or something more bite-sized a “tweetable” or “facebookable”
Missisippi’s percent-chance of finding a contagious person in a…
Classroom: 1-in-4
Football game: 1-in-5
Grocery store: 2-in-3
Place with more than 425 people: 99-in-100
A quick note for the naysayers
So, Nick thinks he’s a doctor now?
Nope. Never have. The calculations made here have zero dependency on understanding medical science. just application of mathematical concepts. It is along the same vein as predicting the weather.
You can’t even get the forecast right…
That’s true. When you take my general forecast for an area and try to apply it specifically to your house, I probably miss. Because I’m not trying to forecast for your specific point. But I’m far from perfect. In fact, even my general forecast is incorrect about three times per season – or about once per month. That means once out of every 20 forecasts, I’m wrong by more than three degrees for the next day. Or get the percent-chance for rain wrong. Or get the timing of precipitation off by more than six hours.
Attempt to – literally – predict future events is not a perfect science.
In this case, I’m not predicting future events. I am making calculations based on current data for current data.
In essence, I’m being asked for solve 2 + 2, instead of 2 + (whatever number the next person who walks into the coffee shop is thinking about).
But the case numbers are exaggerated!
Okay, let’s say they inflated the numbers by 50-percent. For every one case, they counted two. That means the percent-chance that a classroom has one contagious person is 1-in-8. Still not good enough? Let’s say they counted four new cases for every one actual case. The entire medical community was in on it, even the governor! Big conspiracy to ruin America. By all parties. That still puts it around a 1-in-12 chance. One out of every 12 classrooms would have a chance to have a contagious person. even with a giant conspiracy to cover-up the truth at every level of the state government down to local clinics.
The Bottom Line
I really want to drive home the point that the numbers posted here are estimates. While, yes, these estimates based on past research and real science, they still estimates. And estimates need to be treated in a different way than real, actual data.
Real data is, well, real. And should carry more weight when making decisions about your levels of risk.
Estimates should be used to help you make a decision when the real data can’t give you an obvious decision one-way or the other.
I’ll give you an example….
On the news, it is reported that Mississippi “has 59,637 COVID-19 cases and 1,657 deaths” and you think, should I be concerned when I go to the store?
Well the data shows that more than 59,000 people have been – at one point – infected by COVID-19. But how many right now are capable of infecting others – potentially getting you sick? No one can know for sure. So you look for science to make an estimate about the numbers. That estimate shows 32,390. Across the whole state of Mississippi! With more than 3,000,000 people! That is only about 1-percent of the population.
No biggie, right?
Maybe not.
Because 1-percent is 1-out-of-100. So, if you go to a store with 100 people, the estimate is telling you there is a chance someone is capable of infecting others.
What is that chance that your one grocery store is the grocery store with the person in it capable of infecting others? That is what the people at Georgia Tech are trying to quantify for you with their estimate numbers.
They estimate it is a 2-in-3 chance. Two out of every three grocery stores (or places where 100 people are located) will have at elast one person who is capable of infecting others.
So, back to your question, “should I be concerned when I go to the store?”
Hopefully that estimate helps you make the decision where the previous real data may have left you with an incomplete ability to properly make a decision..
Very interesting way to look at it. I wish you would have given an example of one of your calculations. Wouldn’t it be more accurate to say “the chance that you would be in the same building as someone infected with the virus” rather than the chance “that you run into someone that is infected with COVID-19 “